Paris Crypto Day
A full day of cryptography talks in the Paris area.
Home / About
June 21 @ ENS
Jun 1, 2019 • Hoeteck
The next Paris Area Crypto Day will be held on 21.06.19 (Fri) at ENS, co-located with Fête de la Musique.
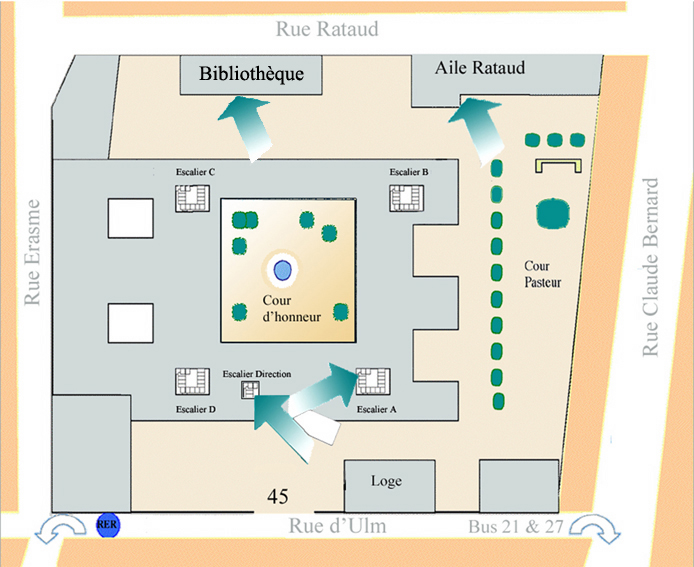
- Amphi Rataud, ENS, 45 rue d’Ulm
- Please register (free). Deadline 17.06.19
Tentative Program
| 09:55–10:00 | Welcome |
| 10:00–11:00 | Jean Paul Degabriele: The Security of Onion Encryption in Tor |
| 11:00–12:00 | Joël Alwen: 2-Party Secure Messaging for Unreliable Channels |
| 12:00–14:00 | Lunch |
| 14:00–14:30 | Aisling Connolly: Freedom of Encryption |
| 14:30–15:00 | Ward Beullens: On Sigma Protocols with Helper for MQ and PKP, Fishy Signature Schemes and More |
| 15:00–15:30 | Rotem Tsabary: Degree 2 is Complete for the Round Complexity of Malicious MPC |
| 15:30–16:00 | Coffee Break |
| 16:00–17:00 | Hoeteck Wee: Encrypted Computation from Lattices |
Organizers. Michel Abdalla, Georg Fuchsbauer and Hoeteck Wee (ENS)
Acknowledgements. ERC CryptoCloud, aSCEND and EfTrEC
Abstracts
The Security of Onion Encryption in Tor
Jean Paul Degabriele (TU Darmstadt)
Tor is a primary tool for maintaining anonymity online. It provides a low-latency, circuit-based, bidirectional secure channel between two parties through a network of onion routers, with the aim of obscuring exactly who is talking to whom, even to adversaries controlling part of the network. Tor relies heavily on cryptographic techniques, yet its onion encryption scheme is susceptible to tagging attacks (Fu and Ling, 2009), which allow an active adversary controlling the first and last node of a circuit to deanonymize with near-certainty. This contrasts with less active traffic correlation attacks, where the same adversary can at best deanonymize with high probability. The Tor project has been actively looking to defend against tagging attacks and its most concrete alternative is proposal 261, which specifies a new onion encryption scheme based on a variable-input-length tweakable cipher. We provide a formal treatment of low-latency, circuit-based onion encryption, relaxed to the unidirectional setting, by expanding existing secure channel notions to the new setting and introducing circuit hiding to capture the anonymity aspect of Tor. We demonstrate that circuit hiding prevents tagging attacks and show proposal 261’s relay protocol is circuit hiding and thus resistant against tagging attacks.
2-Party Secure Messaging for Unreliable Channels
Joël Alwen (Wickr)
Double Ratchet (DR) based protocols have rapidly become the world’s dominant 2-party secure messaging (2SM) paradigm. Yet, despite the paradigm’s wide spread adoption in wild, our cryptographic understanding of it is still evolving.
In this talk, we’ll look at the recent results of Alwen, Coretti and Dodis at Eurocrypt 2019, which focus on building 2SM protocols using the DR paradigm with the explicit goal of obtaining robust, simple and efficient protocols for use in the real world yet provably exhibiting very strong security properties.
We first look at is their new security notion for 2SM. The definition captures (in a clean, intuitive and yet succinct game) both the desired functionality of 2SM, as well as the security properties of Forward Secrecy, Authenticity, Post-Compromise Security and “Resilience to Adversarially Chosen Randomness”. In an effort to further reduce the assumptions about an underlying network’s behavior, the new 2SM definition is also the first to capture the intuitive goal of “Immediate Decryption”; namely that any honestly generated ciphertext can be decrypted immediately upon delivery by the receiver. As this property must hold regardless of the order in which ciphertexts are delivered (and even when arbitrary previous protocol packets were outright dropped) constructions enjoying Immediate Decryption will be far more resilient when used over unreliable transports. This stands in stark contrast to almost all 2SM’s that have been proposed thus far as improvements over the original DR protocol still being used in practice. In fact, essentially all stronger security notions for 2SM’s proposed in those works seem to fundamentally contradict supporting Immediate Decryption. Now, while it is easy to imagine practical settings that require these stronger security notions and/or where the reliability of the underlying transport can be guaranteed, we observe that, to the best of our knowledge, essentially all 2SM protocols actually deployed in practice do indeed support Immediate Decryption. We believe this shows that, often, in practice the added robustness afforded by Immediate Decryption outweighs the value of achieving yet stronger security properties.
Armed with the new security notion, we will take a new look at the DR design paradigm. In particular:
- We describe a modular construction of a DR-based 2SM (and prove its security). For this we use 3, significantly simpler, black-box primitives. In particular, we believe that this approach not only “explains” a wide class of 2SM protocols but that it will also generalize well to the (much more challenging and poorly understood) group secure messaging setting.
- We provide constructions of each of the 3 primitives based on a variety of number-theoretic and black-box primitives. In particular, we obtain: 1) the original DR protocol as used in practice resulting in a new security proof for a 2SM currently used by over 1 billion people. 2) the first provably PQ-secure 2SM. 3) a new highly efficient 2SM with stronger security properties than anything used in practice (yet still enjoying Immediate Decryption).
Finally, we extend the modular construction to include basic public-key
primitives. Using this, we obtain a yet more secure 2SM, albeit at a
moderate cost in efficiency.
Freedom of Encryption
Aisling Connolly (ENS)
Legislation surrounding digital privacy has seen quite an upheaval in recent years. The introduction of the General Data Protection Regulation (GDPR) in the EU, and new resolutions within the United Nations Human Rights Council (UNHRC) have recognized the urgency to include recommendations on the use of encryption to protect the digital identities of citizens. In this work, we meander through the main events in history which have shaped the legislative landscape that encompasses the use of encryption, paying particular attention to recent (post-Snowden) developments.
On Sigma Protocols with Helper for MQ and PKP, Fishy Signature Schemes and More
Ward Beullens (KU Leuven)
This work presents 2 sigma protocols with helper to prove knowledge of:
- A solution to a system of quadratic polynomials
- A solution to an instance of the Permuted Kernel Problem
We then remove the helper from the protocol with a “cut-and-choose” protocol and we apply the Fiat-Shamir transform to obtain signature schemes with security proof in the QROM. We show that the resulting signature schemes, which we call the “MUltivarite quaDratic FIat-SHamir” scheme (MUDFISH) and the “ShUffled Solution to Homogeneous linear SYstem FIat-SHamir” scheme (SUSHSYFISH), are more efficient than existing signatures based on the MQ problem and the Permuted Kernel Problem. We also leverage the ZK-proof for PKP to improve the efficiency of Stern-like Zero Knowledge proofs for lattice statements.
Degree 2 is Complete for the Round Complexity of Malicious MPC
Rotem Tsabary (Weizmann)
We show, via a non-interactive reduction, that the existence of a secure multi-party computation (MPC) protocol for degree-2 functions implies the existence of a protocol with the same round complexity for general functions. Thus showing that when considering the round complexity of MPC, it is sufficient to consider very simple functions.
Our completeness theorem applies in various settings: information theoretic and computational, fully malicious and malicious with various types of aborts. In fact, we give a master theorem from which all individual settings follow as direct corollaries. Our basic transformation does not require any additional assumptions and incurs communication and computation blow-up which is polynomial in the number of players and in S, 2^D, where S,D are the circuit size and depth of the function to be computed. Using one-way functions as an additional assumption, the exponential dependence on the depth can be removed.
As a consequence, we are able to push the envelope on the state of the art in various settings of MPC, including the following cases.
- 3-round perfectly-secure protocol (with guaranteed output delivery) against an active adversary that corrupts less than a quarter of the parties.
- 2-round statistically-secure protocol that achieves security with “selective abort” against an active adversary that corrupts less than half of the parties.
- Assuming one-way functions, 2-round computationally-secure protocol that achieves security with (standard) abort against an active adversary that corrupts less than half of the parties.
Encrypted Computation from Lattices
Hoeteck Wee (CNRS/ENS/PSL)
In this talk, we will survey three cryptographic notions of enabling
computation over encrypted data – attribute-based encryption, fully
homomorphic encryption, and laconic functional evaluation – as well
as their instantiations from lattices.
Venue
45 rue d’Ulm, 75005 Paris, Amphi Rataud: level -1 in the building labeled “Bibliothèque”